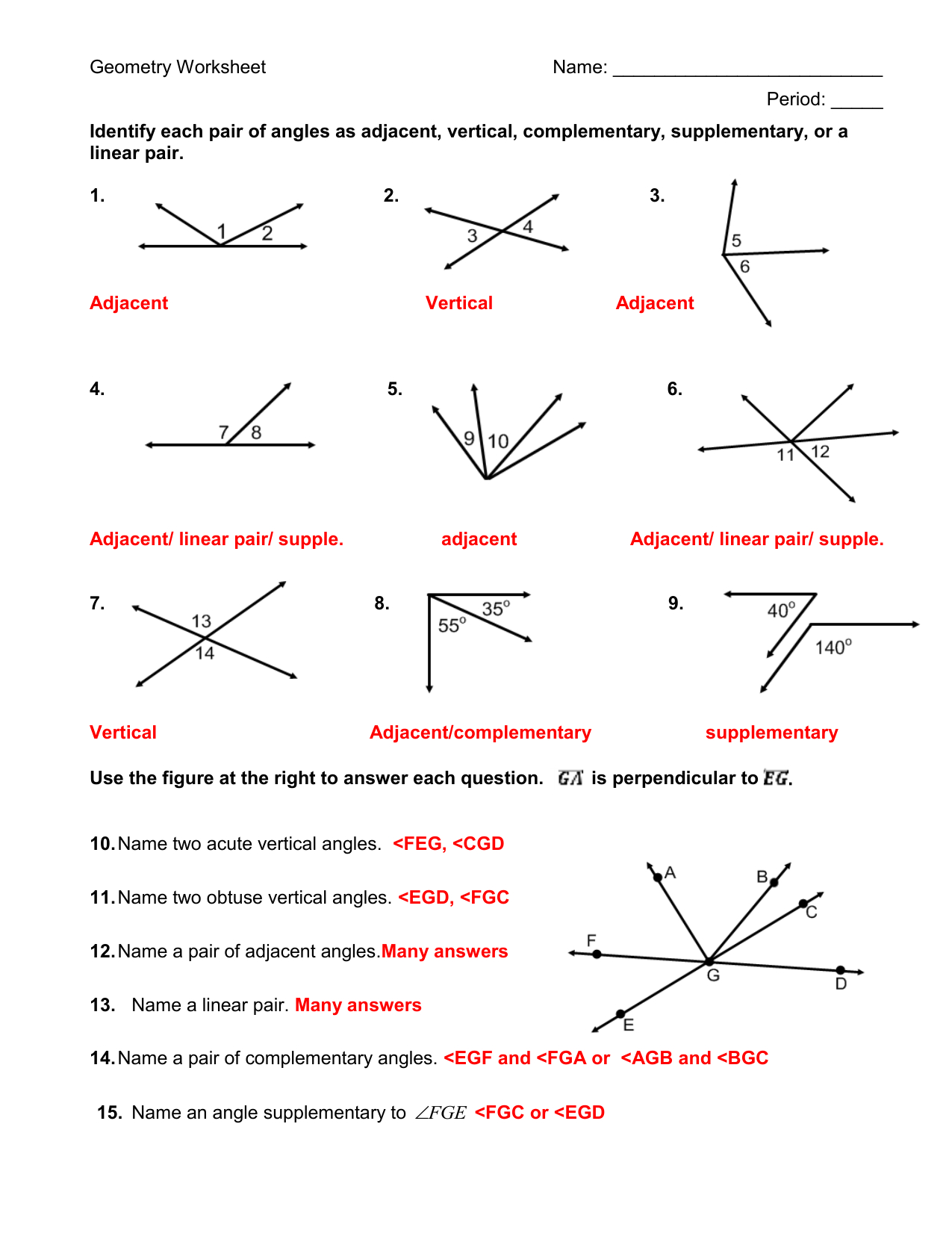
Intersecting Chords Form A Pair Of Supplementary Vertical Angles
Intersecting Chords Form A Pair Of Supplementary Vertical Angles - Web answer 1 i believe the answer to this item is the first choice, true. 15° & 75° are complementary. Supplementary angles add up to 180°. Vertical angles are formed by two intersecting lines. Web here's how you prove the intersecting chords theorem: Web the intersecting chords theorem or just the chord theorem is a statement in elementary geometry that describes a relation of the four line segments created by two intersecting. Worksheets are circle theorems intersecting chords, intersecting chords, angles. On a picture below angles ∠a are vertical, as well as angles ∠b. Web intersecting chords form a pair of supplementary vertical angles? False when chords intersect in a circle the vertical angles formed intercept conruent arcs.
Web angles formed by intersecting chords, vertical angles, and linear pair_#linginthis video explains important relationships among angles formed by. Web vertical angles can be supplementary or complementary. Web supplementary angles are the adjacent angles whose sum is 180° and together form a straight line. False when chords intersect in a circle the vertical angles formed intercept conruent arcs. Web intersecting chords form a pair of supplementary vertical angles? Web here's how you prove the intersecting chords theorem: Just a quick look at the drawing brings to mind. Intersecting chords form a pair of supplementary, vertical angles. Intersecting chords form a pair of congruent vertical angles. Vertical angles are formed and located opposite of.
Web the intersecting chords theorem or just the chord theorem is a statement in elementary geometry that describes a relation of the four line segments created by two intersecting. When the angles are across from each other where the two lines intersect, they are vertical. Intersecting chords form a pair of supplementary, vertical angles. Intersecting chords theorem this is the idea (a,b,c and d are lengths):intersecting chords form a pair of. Web complementary angles add up to 90°. Web any two intersecting lines form two pairs of vertical angles, like this: Web angles formed by intersecting chords, vertical angles, and linear pair_#linginthis video explains important relationships among angles formed by. Web intersecting chords form a pair of supplementary vertical angles? Web answer 1 i believe the answer to this item is the first choice, true. Vertical angles are formed and located opposite of.
Intersecting Chords Form A Pair Of Supplementary Vertical Angles
False when chords intersect in a circle the vertical angles formed intercept conruent arcs. So, here when two intersecting chords of the circle intersect each other at a. When the angles are across from each other where the two lines intersect, they are vertical. Vertical angles are formed by two intersecting lines. Vertical angles are formed and located opposite of.
Intersecting Chords Form A Pair Of Supplementary Vertical Angles
Web here's how you prove the intersecting chords theorem: Web complementary angles add up to 90°. On a picture below angles ∠a are vertical, as well as angles ∠b. False when chords intersect in a circle the vertical angles formed intercept conruent arcs. Intersecting chords theorem this is the idea (a,b,c and d are lengths):intersecting chords form a pair of.
Angle Pair Relationships Adjacent, Vertical, Complementary
Vertical angles are formed and located opposite of. Just a quick look at the drawing brings to mind. Worksheets are circle theorems intersecting chords, intersecting chords, angles. Web the intersecting chords theorem or just the chord theorem is a statement in elementary geometry that describes a relation of the four line segments created by two intersecting. Web intersecting chords form.
Intersecting Chords Form A Pair Of Supplementary Vertical Angles
Web supplementary angles are the adjacent angles whose sum is 180° and together form a straight line. Web vertical angles can be supplementary or complementary. Web intersecting chords form a pair of supplementary vertical angles? Vertical angles are formed by two intersecting lines. Web intersecting chords form a pair of supplementary vertical angles?
Explore the properties of angles formed by two intersecting chords.1
On a picture below angles ∠a are vertical, as well as angles ∠b. So, here when two intersecting chords of the circle intersect each other at a. 15° & 75° are complementary. Web complementary angles add up to 90°. False when chords intersect in a circle the vertical angles formed intercept conruent arcs.
How to Prove the Intersecting Chords Theorem of Euclid 7 Steps
Web supplementary angles are the adjacent angles whose sum is 180° and together form a straight line. Web vertical angles can be supplementary or complementary. Supplementary angles add up to 180°. Web intersecting chords form a pair of supplementary vertical angles? Intersecting chords form a pair of congruent vertical angles.
Pairs Of Angles Worksheet Answers —
So, here when two intersecting chords of the circle intersect each other at a. Intersecting chords form a pair of congruent vertical angles. Web angles formed by intersecting chords, vertical angles, and linear pair_#linginthis video explains important relationships among angles formed by. Just a quick look at the drawing brings to mind. False when chords intersect in a circle the.
Angle relationships between intersecting lines vertical and
Web vertical angles can be supplementary or complementary. Vertical angles are formed and located opposite of. Worksheets are circle theorems intersecting chords, intersecting chords, angles. Web complementary angles add up to 90°. Intersecting chords theorem this is the idea (a,b,c and d are lengths):intersecting chords form a pair of.
Question Video Using Properties of Supplementary Angles and
Web complementary angles add up to 90°. Worksheets are circle theorems intersecting chords, intersecting chords, angles. Web the intersecting chords theorem or just the chord theorem is a statement in elementary geometry that describes a relation of the four line segments created by two intersecting. Web intersecting chords form a pair of supplementary vertical angles? 15° & 75° are complementary.
Intersecting Chords Form A Pair Of Supplementary Vertical Angles
Web answer 1 i believe the answer to this item is the first choice, true. Web any two intersecting lines form two pairs of vertical angles, like this: Web complementary angles add up to 90°. On a picture below angles ∠a are vertical, as well as angles ∠b. Vertical angles are formed and located opposite of.
Intersecting Chords Form A Pair Of Supplementary, Vertical Angles.
Web supplementary angles are the adjacent angles whose sum is 180° and together form a straight line. Web vertical angles can be supplementary or complementary. Just a quick look at the drawing brings to mind. Intersecting chords theorem this is the idea (a,b,c and d are lengths):intersecting chords form a pair of.
Vertical Angles Are Formed And Located Opposite Of.
False when chords intersect in a circle the vertical angles formed intercept conruent arcs. Web here's how you prove the intersecting chords theorem: 15° & 75° are complementary. When the angles are across from each other where the two lines intersect, they are vertical.
Web Any Two Intersecting Lines Form Two Pairs Of Vertical Angles, Like This:
So, here when two intersecting chords of the circle intersect each other at a. Web intersecting chords form a pair of supplementary vertical angles? Web the intersecting chords theorem or just the chord theorem is a statement in elementary geometry that describes a relation of the four line segments created by two intersecting. Worksheets are circle theorems intersecting chords, intersecting chords, angles.
Intersecting Chords Form A Pair Of Congruent Vertical Angles.
On a picture below angles ∠a are vertical, as well as angles ∠b. Web intersecting chords form a pair of supplementary vertical angles? Web answer 1 i believe the answer to this item is the first choice, true. Vertical angles are formed by two intersecting lines.