How To Find The Component Form Of A Vector
How To Find The Component Form Of A Vector - Type the coordinates of the initial and terminal points of vector; Web how do you use vector components to find the magnitude? |v| = √ ( (vx )^2+ ( vy)^2) where vx=vcosθ and vy=vsinθ. Web finding the components of a vector. Web to find the component form of a vector with initial and terminal points: Web a unit circle has a radius of one. Vx=v cos θ vy=vsin θ where v is the magnitude of vector v and can be found using pythagoras. The magnitude of a vector \(v⃗\) is \(20\) units and the direction of the vector is \(60°\) with the horizontal. To find the magnitude of a vector using its components you use pitagora´s theorem. Web now, let’s look at some general calculations of vectors:
V ⃗ ≈ ( \vec v \approx (~ v ≈ ( v, with, vector, on top, approximately. Web when given the magnitude (r) and the direction (theta) of a vector, the component form of the vector is given by r (cos (theta), sin (theta)). Cosine is the x coordinate of where you intersected the unit circle, and sine is the y coordinate. The magnitude of vector v is represented by |v|,. Web therefore, the formula to find the components of any given vector becomes: Web find the component form of v ⃗ \vec v v v, with, vector, on top. Web looking very closely at these two equations, we notice that they completely define the vector quantity a; Vx=v cos θ vy=vsin θ where v is the magnitude of vector v and can be found using pythagoras. Web the component form of a vector is given as < x, y >, where x describes how far right or left a vector is going and y describes how far up or down a vector is going. Web how do you use vector components to find the magnitude?
Consider in 2 dimensions a. Web now, let’s look at some general calculations of vectors: Web the component form of a vector is given as < x, y >, where x describes how far right or left a vector is going and y describes how far up or down a vector is going. They specify both the magnitude and the direction of a. Web finding the components of a vector. |v| = √ ( (vx )^2+ ( vy)^2) where vx=vcosθ and vy=vsinθ. Web the component form of the vector formed by the two point vectors is given by the components of the terminal point minus the corresponding components of the. Vx=v cos θ vy=vsin θ where v is the magnitude of vector v and can be found using pythagoras. Or if you had a vector of magnitude one, it would be. Web to find the component form of a vector with initial and terminal points:
Component Form Of A Vector
They specify both the magnitude and the direction of a. Cosine is the x coordinate of where you intersected the unit circle, and sine is the y coordinate. Type the coordinates of the initial and terminal points of vector; Web to find the component form of a vector with initial and terminal points: Vx=v cos θ vy=vsin θ where v.
How To Find Component Form Of A Vector Given Magnitude And Direction
Type the coordinates of the initial and terminal points of vector; The magnitude of vector v is represented by |v|,. Consider in 2 dimensions a. Round your final answers to the nearest hundredth. Web looking very closely at these two equations, we notice that they completely define the vector quantity a;
Component Vector ( Video ) Calculus CK12 Foundation
Type the coordinates of the initial and terminal points of vector; The magnitude of vector v is represented by |v|,. Web improve your math knowledge with free questions in find the component form of a vector and thousands of other math skills. Consider in 2 dimensions a. Web find the component form of v ⃗ \vec v v v, with,.
How to write component form of vector
Type the coordinates of the initial and terminal points of vector; To find the magnitude of a vector using its components you use pitagora´s theorem. V ⃗ ≈ ( \vec v \approx (~ v ≈ ( v, with, vector, on top, approximately. Web to find the component form of a vector with initial and terminal points: If and are two.
How To Find Component Form Of A Vector Given Magnitude And Direction
Round your final answers to the nearest hundredth. Web finding the components of a vector. Web the component form of the vector formed by the two point vectors is given by the components of the terminal point minus the corresponding components of the. |v| = √ ( (vx )^2+ ( vy)^2) where vx=vcosθ and vy=vsinθ. Consider in 2 dimensions a.
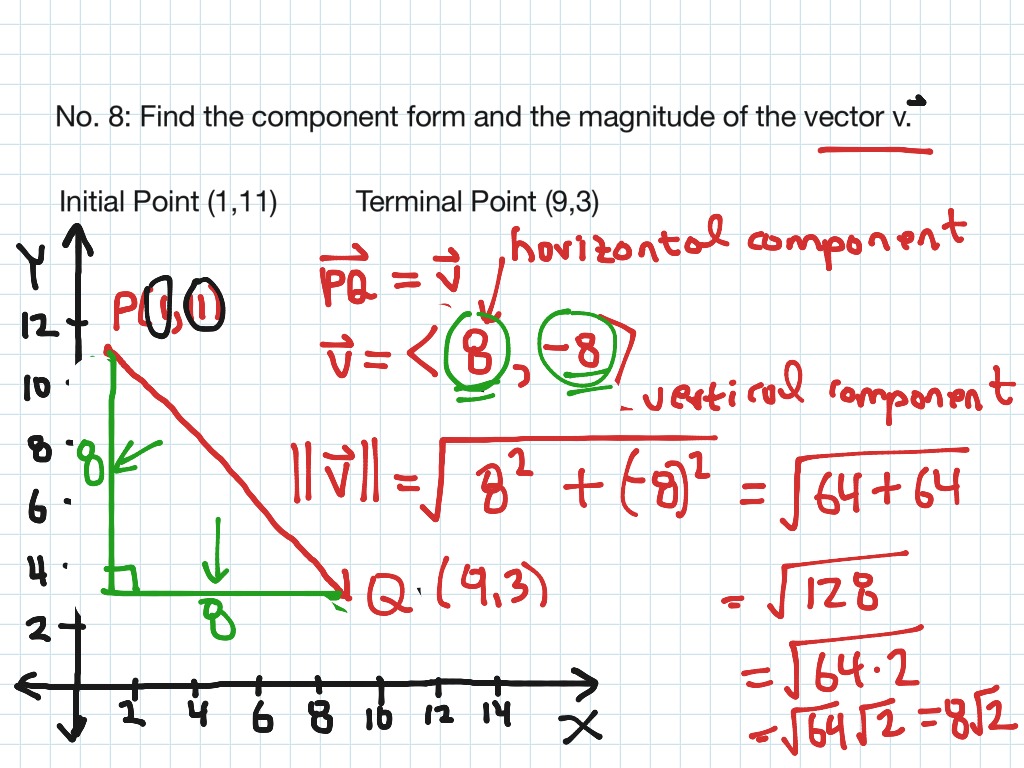
6.3 No. 8 Finding the Component Form and the Magnitude of a Vector
V ⃗ ≈ ( \vec v \approx (~ v ≈ ( v, with, vector, on top, approximately. Web find the component form of v ⃗ \vec v v v, with, vector, on top. Web to find the component form of a vector with initial and terminal points: Cosine is the x coordinate of where you intersected the unit circle, and.
How To Find Component Form Of A Vector Given Initial And Terminal Points
Consider in 2 dimensions a. Web the component form of a vector is given as < x, y >, where x describes how far right or left a vector is going and y describes how far up or down a vector is going. V ⃗ ≈ ( \vec v \approx (~ v ≈ ( v, with, vector, on top, approximately..
PC 6.3 Notes Example 8 Find the Component Form of a Vector YouTube
The magnitude of a vector \(v⃗\) is \(20\) units and the direction of the vector is \(60°\) with the horizontal. Round your final answers to the nearest hundredth. Web finding the components of a vector (opens a modal) comparing the components of vectors (opens a modal) practice. Examples, solutions, videos, and lessons to help precalculus students learn about component vectors.
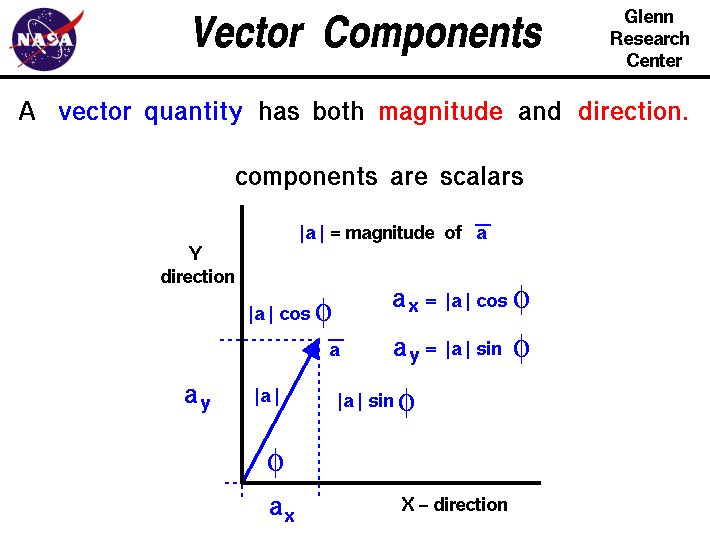
Vector Components
Web the following formula is applied to calculate the magnitude of vector v: Or if you had a vector of magnitude one, it would be. Type the coordinates of the initial and terminal points of vector; Web now, let’s look at some general calculations of vectors: Web when given the magnitude (r) and the direction (theta) of a vector, the.
Order Essay from Experienced Writers with Ease how to write component
Web finding the components of a vector. The magnitude of a vector \(v⃗\) is \(20\) units and the direction of the vector is \(60°\) with the horizontal. Web finding the components of a vector (opens a modal) comparing the components of vectors (opens a modal) practice. Web improve your math knowledge with free questions in find the component form of.
Web When Given The Magnitude (R) And The Direction (Theta) Of A Vector, The Component Form Of The Vector Is Given By R (Cos (Theta), Sin (Theta)).
The magnitude of a vector \(v⃗\) is \(20\) units and the direction of the vector is \(60°\) with the horizontal. Web therefore, the formula to find the components of any given vector becomes: Vx=v cos θ vy=vsin θ where v is the magnitude of vector v and can be found using pythagoras. Type the coordinates of the initial and terminal points of vector;
The Magnitude Of Vector V Is Represented By |V|,.
Web to find the component form of a vector with initial and terminal points: They specify both the magnitude and the direction of a. Cosine is the x coordinate of where you intersected the unit circle, and sine is the y coordinate. Web find the component form of v ⃗ \vec v v v, with, vector, on top.
Web How Do You Use Vector Components To Find The Magnitude?
|v| = √ ( (vx )^2+ ( vy)^2) where vx=vcosθ and vy=vsinθ. Web finding the components of a vector. Web a unit circle has a radius of one. To find the magnitude of a vector using its components you use pitagora´s theorem.
Or If You Had A Vector Of Magnitude One, It Would Be.
Web now, let’s look at some general calculations of vectors: Consider in 2 dimensions a. Adding vectors in magnitude and direction form. Web looking very closely at these two equations, we notice that they completely define the vector quantity a;