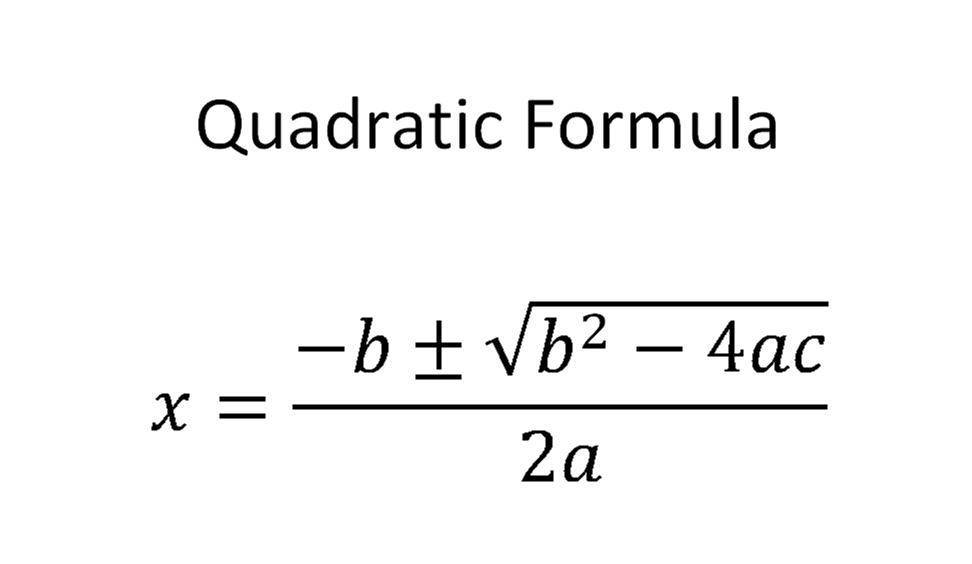Gradient Quadratic Form

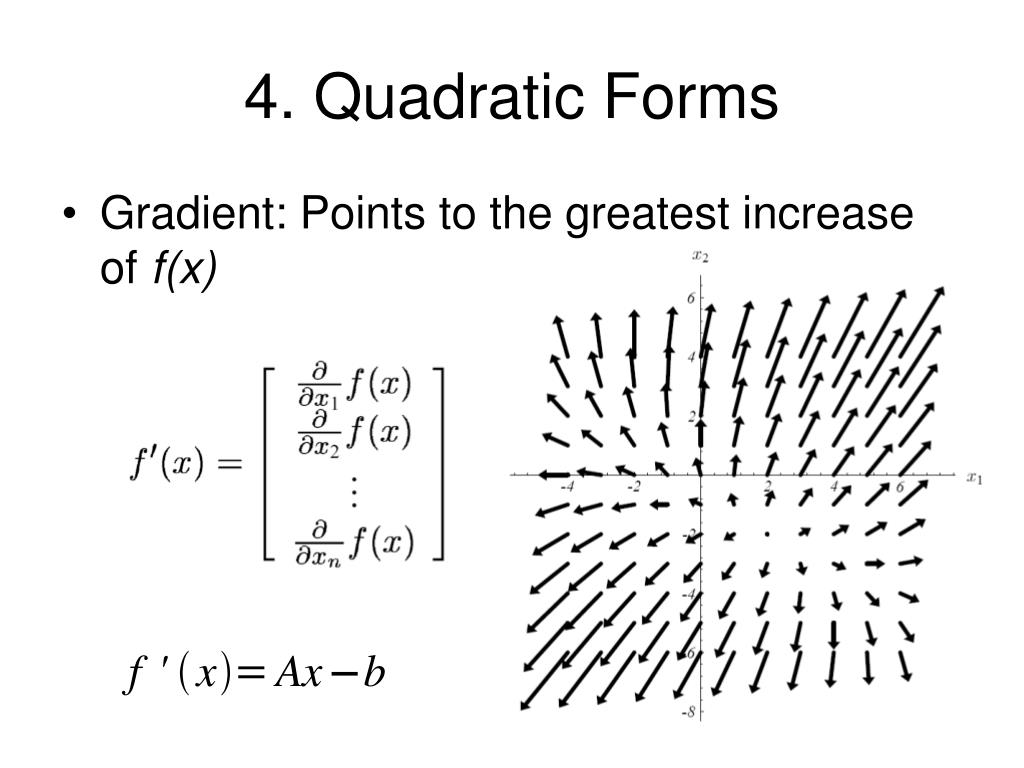
Gradient Quadratic Form - For f aﬃne, i.e., f(x) = atx+b, we have ∇f(x) = a (independent. Web converting from quadratic form to standard form is quite common, so you can also check out this helpful video for another example. Return to the table of. Web the idea of quadratic forms is introduced and used to derive the methods of steepest descent, conjugate directions, and conjugate gradients. Powered by x x y y a squared a. I am taking derivative of xtax, x ∈irn x t a x,. Web introduction quadratic forms are homogeneous quadratic polynomials in n variables. Where a is a symmetric 3 3 matrix. R¯n → r given by the quadratic form f(x)= x'ax , where a ∈r¯n×¯n is square matrix, is given by ∇xf= ax+a'x. (5 answers) closed 3 years ago.

Web introduction quadratic forms are homogeneous quadratic polynomials in n variables. [noun] a homogeneous polynomial (such as x2 + 5xy + y2) of the second degree. B b is the coefficient in front of the x x , so here b =. To finish our graph, we need to find another point on the curve. In the cases of one, two, and three variables they are called unary, binary, and ternary and. Web 1 this question already has answers here : Web learn how to graph any quadratic function that is given in standard form. Where a is a symmetric 3 3 matrix. The function f (x,y) =x^2 * sin (y) is a three dimensional function with two inputs and one output and the gradient of f is a two dimensional vector valued function. Return to the table of.

Web learn how to graph any quadratic function that is given in standard form. (5 answers) closed 2 years ago. Web quadratic form as f(x) = f(x 1;x 2;x 3) = [x 1 x 2 x 3] 2 6 4 a 11 a 12 a 13 a 21 22 23 a 31 a 32 a 33 3 7 5 2 6 4 x 1 x 2 x 3 3 7 5= xax; Web introduction quadratic forms are homogeneous quadratic polynomials in n variables. How to take the gradient of the quadratic form? In the cases of one, two, and three variables they are called unary, binary, and ternary and. Web the idea of quadratic forms is introduced and used to derive the methods of steepest descent, conjugate directions, and conjugate gradients. For f aﬃne, i.e., f(x) = atx+b, we have ∇f(x) = a (independent. Where a is a symmetric 3 3 matrix. Web how to take the gradient of the quadratic form?

Index of quadratic form

Powered by x x y y a squared a. [noun] a homogeneous polynomial (such as x2 + 5xy + y2) of the second degree. Web the idea of quadratic forms is introduced and used to derive the methods of steepest descent, conjugate directions, and conjugate gradients. Where a is a symmetric 3 3 matrix. The standard form of a.

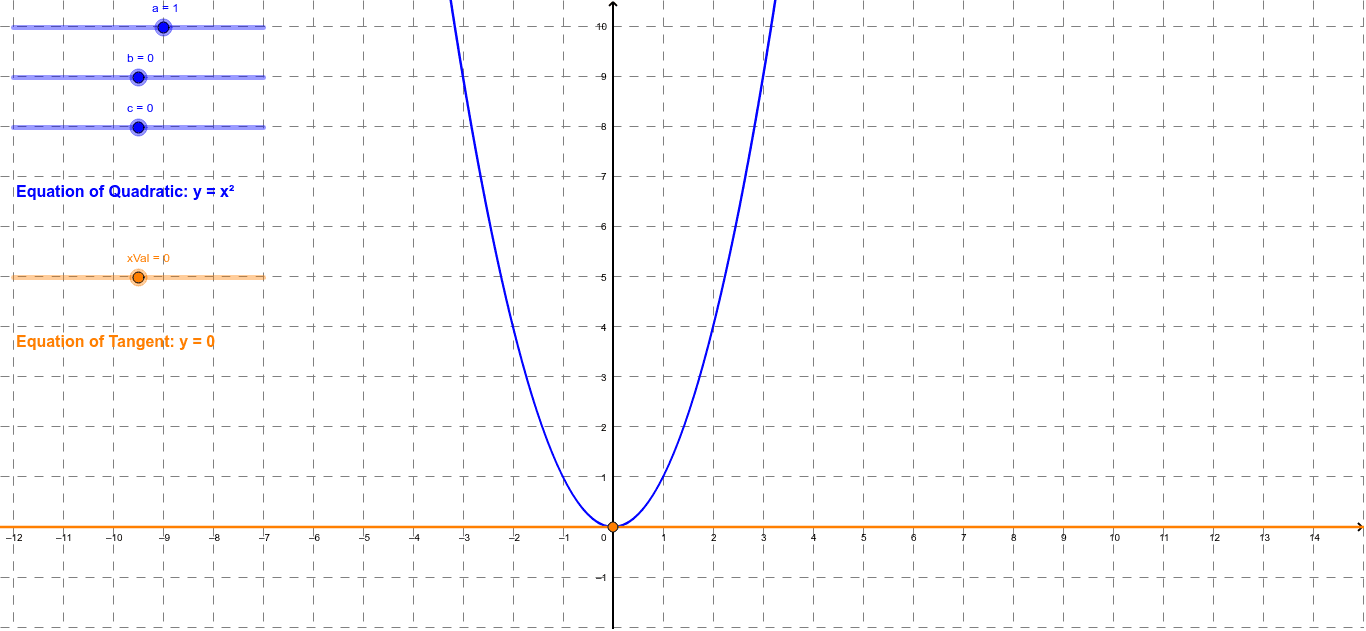
37 Finding the Gradient of a Quadratic Function at a Point from the

(5 answers) closed 2 years ago. (5 answers) closed 3 years ago. The function f (x,y) =x^2 * sin (y) is a three dimensional function with two inputs and one output and the gradient of f is a two dimensional vector valued function. The standard form of a. To finish our graph, we need to find another point on the.

Gradient Texture Blender Cycles memo

[noun] a homogeneous polynomial (such as x2 + 5xy + y2) of the second degree. Web gradient of aﬃne and quadratic functions you can check the formulas below by working out the partial derivatives. Web converting from quadratic form to standard form is quite common, so you can also check out this helpful video for another example. Web the general.

Finding the Gradient of a Quadratic Function GeoGebra

B b is the coefficient in front of the x x , so here b =. Web how to take the gradient of the quadratic form? Web the idea of quadratic forms is introduced and used to derive the methods of steepest descent, conjugate directions, and conjugate gradients. Return to the table of. [noun] a homogeneous polynomial (such as x2.

JEE Quadratic Expressions Brilliant Math & Science Wiki

PPT Conjugate Gradient PowerPoint Presentation, free download ID

To finish our graph, we need to find another point on the curve. Web learn how to graph any quadratic function that is given in standard form. B b is the coefficient in front of the x x , so here b =. [noun] a homogeneous polynomial (such as x2 + 5xy + y2) of the second degree. Web quadratic.

Gradient at any point of a Quadratic Curve YouTube

Where a is a symmetric 3 3 matrix. (5 answers) closed 2 years ago. How to take the gradient of the quadratic form? Web the general form of a quadratic function is f (x) = a x 2 + b x + c f (x) = a x 2 + b x + c where a, b, a, b, and.

4 2B Graphing Quadratic Equations in Intercept Form

Web the idea of quadratic forms is introduced and used to derive the methods of steepest descent, conjugate directions, and conjugate gradients. Web introduction quadratic forms are homogeneous quadratic polynomials in n variables. Web the idea of quadratic forms is introduced and used to derive the methods of steepest descent, conjugate directions, and conjugate gradients. Web gradient of aﬃne and.

CalcBLUE 2 Ch. 6.3 Derivatives of Quadratic Forms YouTube

The function f (x,y) =x^2 * sin (y) is a three dimensional function with two inputs and one output and the gradient of f is a two dimensional vector valued function. To finish our graph, we need to find another point on the curve. (5 answers) closed 3 years ago. Web quadratic form as f(x) = f(x 1;x 2;x 3).

How do you solve 3x^2 8x + 5 = 0 using the quadratic formula? Socratic

To finish our graph, we need to find another point on the curve. How to take the gradient of the quadratic form? Web prove that the gradient ∇xf ( 33.29) of the function f: Web the idea of quadratic forms is introduced and used to derive the methods of steepest descent, conjugate directions, and conjugate gradients. Web learn how to.

Web Converting From Quadratic Form To Standard Form Is Quite Common, So You Can Also Check Out This Helpful Video For Another Example.

(5 answers) closed 3 years ago. [noun] a homogeneous polynomial (such as x2 + 5xy + y2) of the second degree. To finish our graph, we need to find another point on the curve. The standard form of a.

Web Prove That The Gradient ∇Xf ( 33.29) Of The Function F:

(5 answers) closed 2 years ago. Web graphing a quadratic equation. Return to the table of. How to take the gradient of the quadratic form?

I Am Taking Derivative Of Xtax, X ∈Irn X T A X,.

For f aﬃne, i.e., f(x) = atx+b, we have ∇f(x) = a (independent. B b is the coefficient in front of the x x , so here b =. Where a is a symmetric 3 3 matrix. Web introduction quadratic forms are homogeneous quadratic polynomials in n variables.

Web The Idea Of Quadratic Forms Is Introduced And Used To Derive The Methods Of Steepest Descent, Conjugate Directions, And Conjugate Gradients.

Web gradient of aﬃne and quadratic functions you can check the formulas below by working out the partial derivatives. Web the general form of a quadratic function is f (x) = a x 2 + b x + c f (x) = a x 2 + b x + c where a, b, a, b, and c c are real numbers and a ≠ 0. Web the idea of quadratic forms is introduced and used to derive the methods of steepest descent, conjugate directions, and conjugate gradients. In the cases of one, two, and three variables they are called unary, binary, and ternary and.